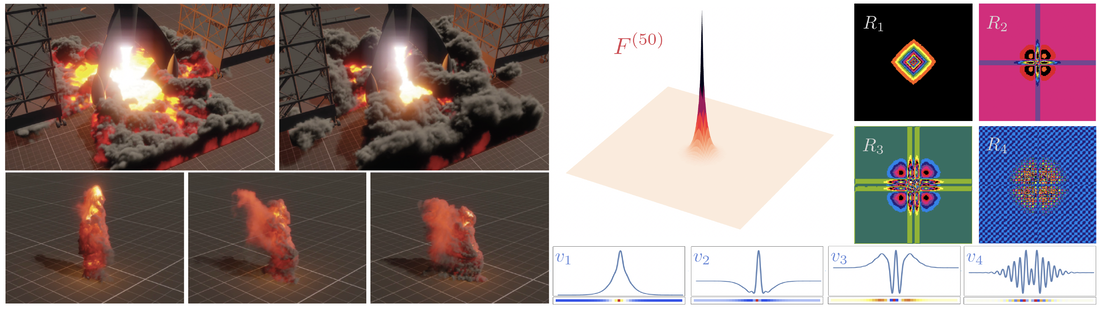
Compact Poisson Filters
for Fast Fluid Simulation
A. H. Rabbani*, J. Guertin*, D. Rioux-Lavoie*, A. Schoentgen*,
K. Tong§, A. Sirois-Vigneux† , D, Nowrouzezahrai†
SIGGRAPH '22: ACM SIGGRAPH 2022 Conference Proceedings
K. Tong§, A. Sirois-Vigneux† , D, Nowrouzezahrai†
SIGGRAPH '22: ACM SIGGRAPH 2022 Conference Proceedings
|
* La Forge R&D Ubisoft Montreal
|
† McGill University
|
§ University of British Columbia
|