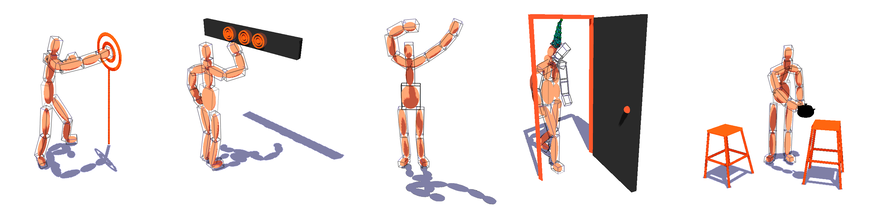
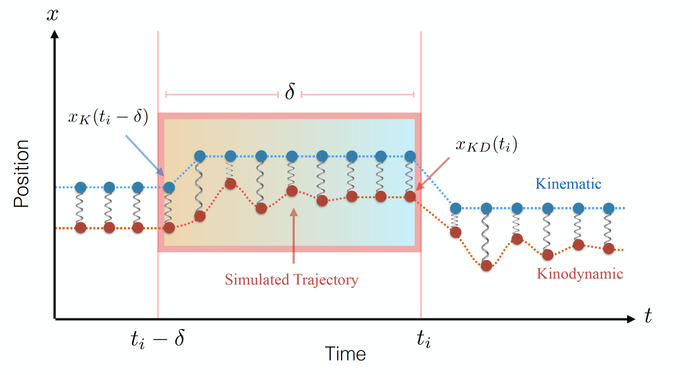
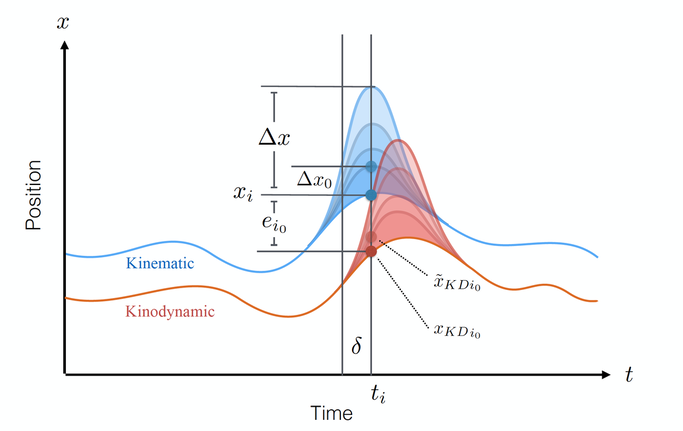
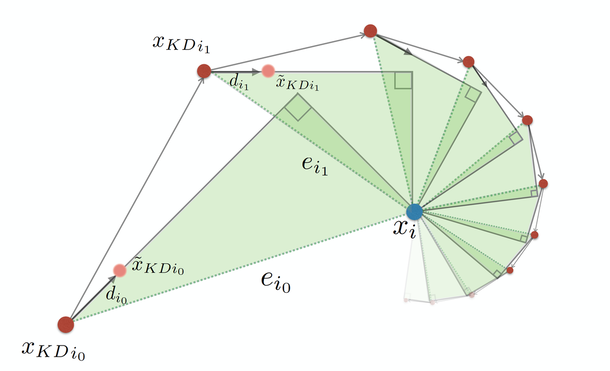
Inverse Kinodynamics
Editing and Constraining Kinematic Approximations of Dynamic Motion
Journal
Paul G. Kry*, Cyrus Rahgoshay*, Amir H. Rabbani*, Karan Singh†
Computers & Graphics, 2012
Conference
Cyrus Rahgoshay*, Amir H. Rabbani*, Karan Singh†, Paul G. Kry*
Graphics Interface, 2012
BEST PAPER
Paul G. Kry*, Cyrus Rahgoshay*, Amir H. Rabbani*, Karan Singh†
Computers & Graphics, 2012
Conference
Cyrus Rahgoshay*, Amir H. Rabbani*, Karan Singh†, Paul G. Kry*
Graphics Interface, 2012
BEST PAPER
|
*McGill University
|
†University of Toronto
|